内容介绍
看见函数是一款方便函数学习的图示app,只要输入你需要知道的函数图公式,就会呈现出对应的函数图,方便学生的学习与思考。支持加、减、乘、除、幂函数、指数函数、对数函数、三角函数,反三角函数等所有初等函数,另外还支持绝对值、最小、最大等函数。绘制的函数曲线可以平移和缩放。放大时最小坐标单位为0.001。
【看见函数app介绍】
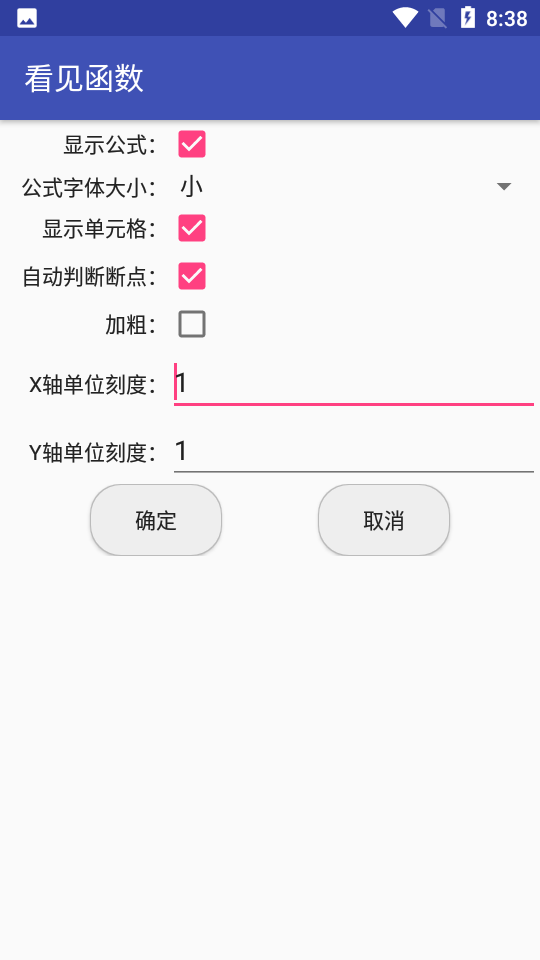
新增函数图像的操作方法也非常的简单,还能对图像进行修改、参数设置等操作。
从不同的视角观看函数图像,还能利用软件进行函数式计算,帮助计算函数结果。
能够将绘制的函数图像存储下来,比如各类常见函数图像,在使用时直接查询即可。
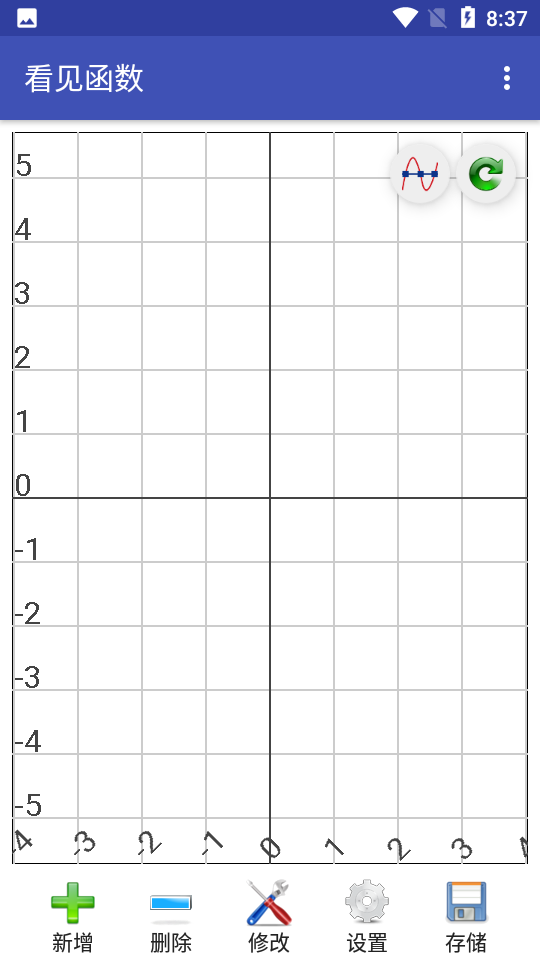
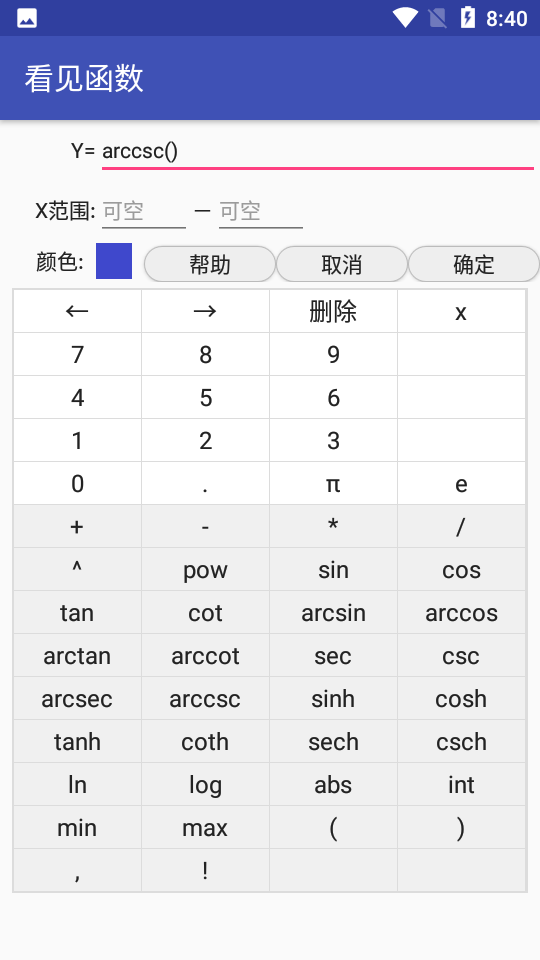
有着自动制作函数图像的功能,您只需要输入函数图像的公式,然后就会自动绘制。
在图像上点击某一个函数点,还能查看不同参数的数值,轻松得到正确数值。
能够直接查看存储的函数图像,并且还能进行历史查询,容易管理存储的图像。
【看见函数app操作方法】
该程序根据用户输入的函数方程绘制函数曲线。
支持加、减、乘、除、幂函数、指数函数、对数函数、三角函数,反三角函数等所有初等函数,
另外还支持绝对值、最小、最大等函数。
绘制的函数曲线可以平移和缩放。放大时最小坐标单位为0.001。
【看见函数app函数的定义】
给定一个数集A,假设其中的元素为x。现对A中的元素x施加对应法则f,记作f(x),得到另一数集B。假设B中的元素为y。则y与x之间的等量关系可以用y=f(x)表示。我们把这个关系式就叫函数关系式,简称函数。
函数概念含有三个要素:定义域A、值域C和对应法则f。其中核心是对应法则f,它是函数关系的本质特征。
函数(function),最早由中国清朝数学家李善兰翻译,出于其著作《代数学》。之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个量的变化而变化,或者说一个量中包含另一个量。
函数的定义通常分为传统定义和近代定义,函数的两个定义本质是相同的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合、映射的观点出发。
首先要理解,函数是发生在集合之间的一种对应关系。然后,要理解发生在A、B之间的函数关系不止且不止一个。最后,要重点理解函数的三要素。
达到当天最大量API KEY 超过次数限制